mirrorguy
 
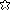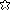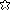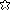
文章: 45
 |
 于 2002-06-13 13:01   
Assuming the incoming and outgoing water rates are the same.
Denote the size of the main tank to be M, the size of plastic box to be S. Assume the percentage of new water in the main tank is f(t), a function of time t.
Then during a certain time period from t to t+t1, the balance of new water is given by
S t1 - S t1 f(t) = M f(t+t1) - M f(t)
Let t1 --> 0, we obtain
S (1- f(t)) = M f'(t).
The initial condition is f(0) = 0. Solve the equation we have
f(t) = 1 - e^(-S t/M)
Finally, new water in the main tank is
M [ 1 - e^(-S/M) ].
For the problem proposed by iczfirz, M = 150L, S = 50L. Substitute them into the formula, we have
150 [1 - e^(-1/3) ] = 42.5 L
This means iczfirz had 42.5L new water remaining in the main tank. Waaa...., that's more than everybody's expectation!!!
So, next time if you want to change water by using iczfirz's approach, then just use the formula:
M [ 1 - e^(-S/M) ].
mirrorguy 修改于 2002-06-13 20:52
|
顯示適合列印的版本 
寄給朋友
